BloomFilter概念
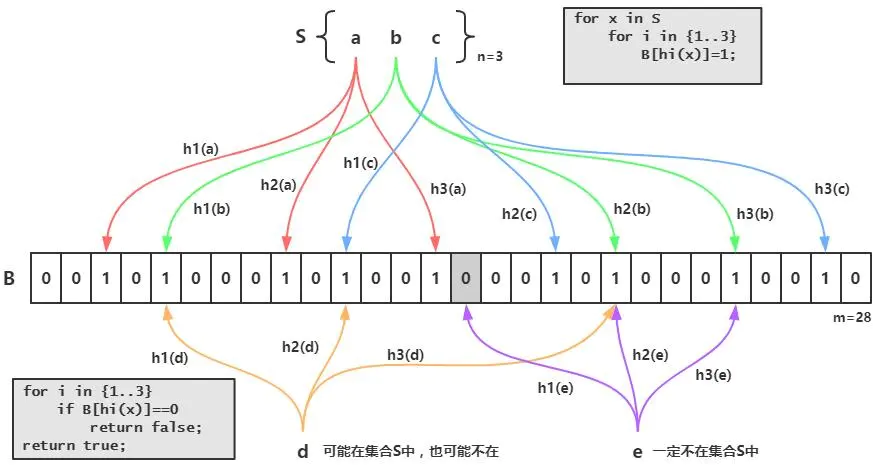
布隆过滤器的原理是,当一个元素被加入集合时,通过K个散列函数将这个元素映射成一个位数组中的K个点,把它们置为1。检索时,我们只要看看这些点是不是都是1就(大约)知道集合中有没有它了:如果这些点有任何一个0,则被检元素一定不在;如果都是1,则被检元素很可能在。这就是布隆过滤器的基本思想。 Bloom Filter跟单哈希函数Bit-Map不同之处在于:Bloom Filter使用了k个哈希函数,每个字符串跟k个bit对应。从而降低了冲突的概率。
缓存穿透
意思是我写一个不存在的ID,一直去访问redis,没命中的话,就会都落到数据库,为了避免这种问题,需要先判断下元素在不在,不在的话,直接返回,降低数据库的压力。
bloomfilter的不足
bloom filter之所以能做到在时间和空间上的效率比较高,是因为牺牲了判断的准确率、删除的便利性
- 存在误判,可能要查到的元素并没有在容器中,但是hash之后得到的k个位置上值都是1。如果bloom filter中存储的是黑名单,那么可以通过建立一个白名单来存储可能会误判的元素。
- 删除困难。一个放入容器的元素映射到bit数组的k个位置上是1,删除的时候不能简单的直接置为0,可能会影响其他元素的判断。可以采用Counting Bloom Filter
我在项目是怎么做的
const hashers = (value, times) => {
const hash = crypto.createHash('sha1').update(value).digest();
const h1 = hash.readUInt32BE(8);
const h2 = hash.readUInt32BE(12);
const hashes = [];
//only two hash functions are necessary to effectively implement a Bloom filter without
//any loss in the asymptotic false positive probability
for (let i = 1; i <= times; i++) {
hashes.push(h1 + h2 * i);
}
return hashes;
};
class BloomFilter {
constructor({ cache, size = 1000000, errorRate = 0.005 }) {
if (cache) {
const [mark, m, k, e, bits] = cache;
this._m = m;
this._k = k;
this._e = e;
this._bits = new Bits(0, bits);
} else {
this._m = Math.round((-1 * size * Math.log(errorRate)) / LN2_SQUARE);
if (this._m % BYTE_LEN) {
this._m += (BYTE_LEN - (this._m % BYTE_LEN));
}
this._k = Math.max(1, Math.round(this._m / size * Math.LN2));
this._e = errorRate;
this._bits = new Bits();
}
}
add(value) {
if (isInteger(value)) {
this._bits.set(value);
} else {
hashers(value, this._k).forEach(_ => this._bits.set(_ % this._m));
}
return this;
}
has(value) {
if (isInteger(value)) {
return this._bits.get(value);
}
return hashers(value, this._k).every(_ => this._bits.get(_ % this._m));
}
}
module.exports = BloomFilter;
总结
从实现上说,guava也有对应实现了,这里是用node写的,这里的hash函数是参照下面参考文件来设置
【1】 https://www.eecs.harvard.edu/~michaelm/postscripts/rsa2008.pdf